# 6.4.3. Shortest-Paths Problems

alg

dijstra@datascience
Single-source shortest-paths problem
- Dijkstra’s algorithm
  - Only nonnegative-weight edges are present.
- Bellman-Ford algorithm
  - Negative-weight edges may be present, but there are no negative-weight cycles.
Single-destination shortest-paths problem
Singe-pair shortest-path problem
All-pairs shortest-paths problem
- Floyd-Warshall algorithm
  - Negative-weight edges may be present, but there are no negative-weight cycles.
- Johnson’s algorithm for sparse graphs
  - Negative-weight edges may be present, but there are no negative-weight cycles.
The optimal-substructure property of shortest paths
- Subpaths of shortest paths are shortest paths!

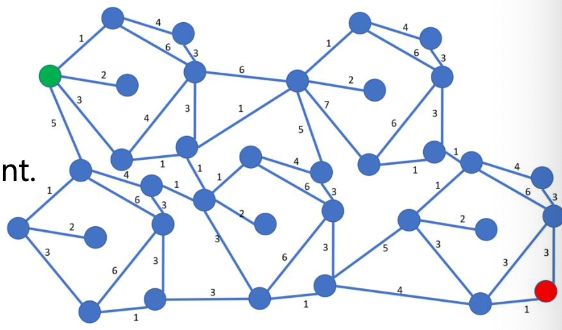
# Single-Source Shortest Path

Problem
- Given a weighted directed graph G = (V, E) with a weighting function w(e) (w(e) ≥ 0 for the edges in G), and a source vertex v_0, find a shortest path from v_0 to each of the remaining vertices of G.
Note
- The case of an undirected graph can be handled by simply replacing each undirected edge e = (u, v) of length w(e) by two directed edges (u, v) and (v, u), each of the same length.
- Only the case of a directed graph whose weights are positive (or nonnegative) is handled by the Dijkstra’s algorithm. For a graph that allows a negative weight, the Bellman-Ford algorithm is one to be used.
- Before learning the single-source shortest path algorithm that builds some tree, recall how the breadth first search tries to build a BFS tree.
- A breadth first search tree
- A tree built by the Dijkstra’s algorithm

# Dijkstra’s Single-Source Shortest Path Algorithm

A greedy approach
- Generate the shortest paths in non-decreasing order of lengths!

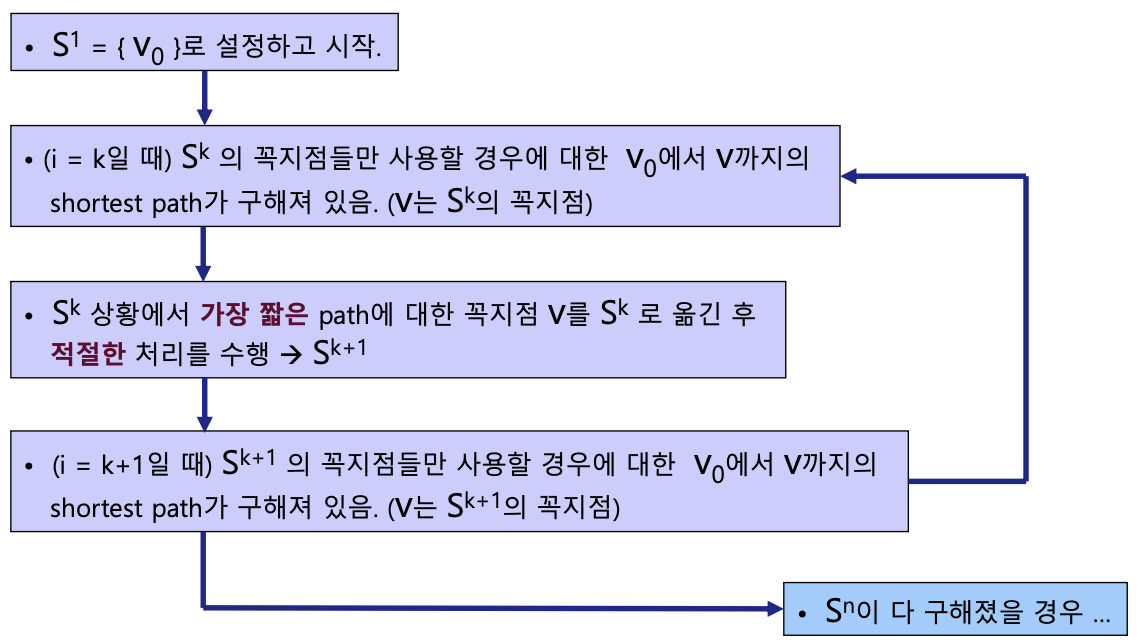
$S^1={ v_0 }$로 설정하고 시작.
($i=k$일 때) $S^{k$의 꼭지점들만 사용할 경우에 대한 $v_0$에서 $v$까지의 shortest path가 구해져 있음. ($v$는 $S}k$의 꼭지점)
$S^{k$상황에서 가장 짧은 path에 대한 꼭지점 $v$를 $S}k$로 옮긴 후 적절한 처리를 수행 → S^{k+1}
($i = k+1$일 때) S^{k+1} 의 꼭지점들만 사용할 경우에 대한 $v_0$에서 $v$까지의 shortest path가 구해져 있음. ($v$는 $S^{k+1}$의 꼭지점)
- 다시 2. 로 감
S_n 이 다 구해졌을 경우

# From Prof. Kenji Ikeda's Home Page

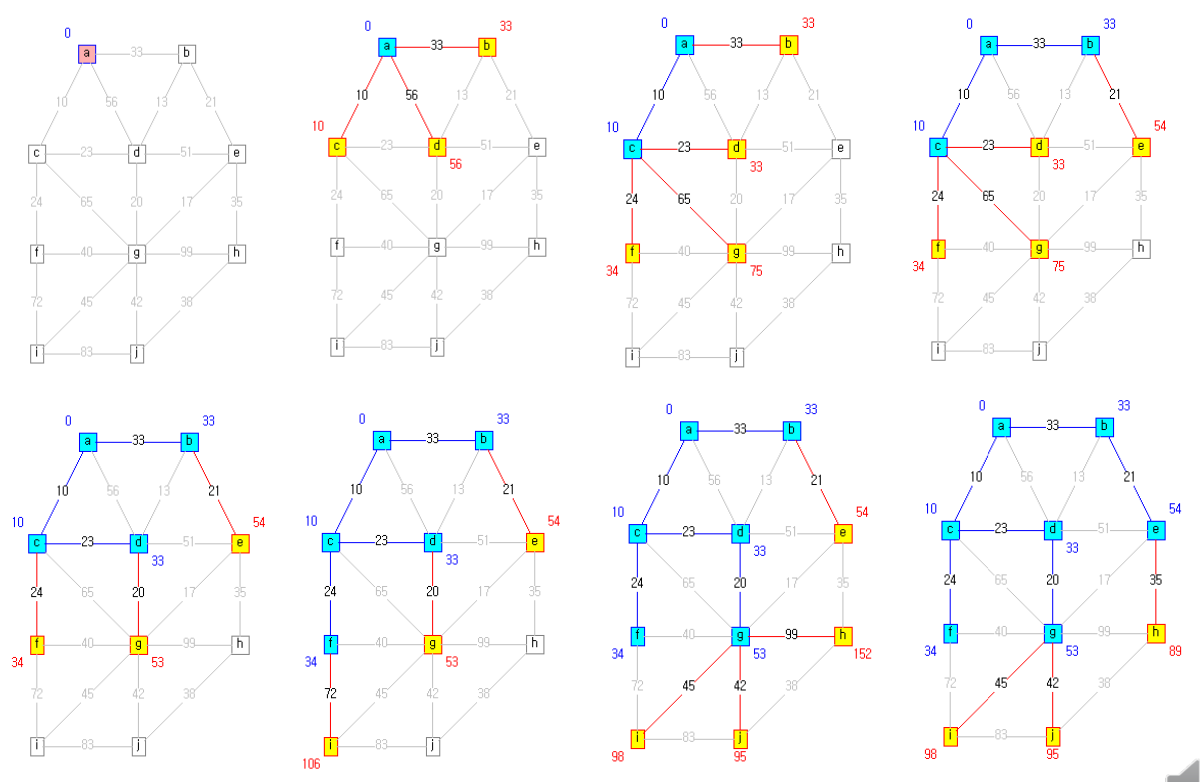
# Dijkstra’s Algorithm

(from Introduction to Algorithms by T. Cormen)

A directed graph with nonnegative weight G(V, E) with w: E→ [0,∞) and source s
Two components for each vertex v
- v.d: an upper bound on the weight of a shortest path from s to v (a shortest path estimate)
- v.π: the predecessor of v in the (current) shortest path
```
Initialize-Single-Source(G,s)
  for each vertex v in G.V
	  v.d = infinite
	  v.pi = NIL
  s.d = 0
```
Relaxation
- The process of relaxing an edge (u, v) consists of testing whether we can improve the shortest path to v found so far by going through u and, if so, updating v.d and v.π.
```
Relax(u,v,w)
if v.d > u.d + w(u,v)
	v.d = u.d + w(u,v)
	v.pi = u
```
  - 아직 shortest path를 찾지 못한 vertex v에 대해
  - 새롭게 선택된 vertex u에 adjacent한 vertex v에 대해

# Dijkstra’s Single-Source Shortest Path Algorithm

Dijkstra’s algorithm
- Maintains a set S of vertices whose final shortest-path weight from the source s have already been determined.
  1. Select repeatedly the vertex u in V-S with the minimum shortest-path estimate
  2. adds u to S
  3. relaxes all edges leaving u.
```
Dijkstra(G,w,s)
1  Initialize-Single-Source(G,s)
2  S = zero-set
3  Q = G.V
4  while Q != zero-set
5    u= extract-min(Q)
6    S= S U {u}
7    for each vertex v in G.Adj[u]
8      Relax(u,v,w)
```
- When the algorithm adds a vertex u to the set S, u.d is the final shortest-path weight from s to u.
- 계산과정 예
Correctness of Dijkstra’s algorithm
- Theorem
  - Dijkstra algorithm, run on a weighted, directed graph $ G=(V,E)$ with nonnegative weight function w : E \rightarrow R and source s, terminates with v.d = \delta(s,v) \forall vertices v \in V
- Loop invariant
  - At the start of each iteration of the while loop of lines 4-8, v.d = \delta(s,v) for each vertex v \in S
- A key in the proof
  - to show that for each vertex u \in V, we have u.d = \delta(s,u) at the time when u is added to set S
  - Suppose for contradiction that u be the first vertex for which u.d \neq \delta(s,u) when it is added to set S
    Dijkstra(G,w,s) 1 Initialize-Single-Source(G,s) 2 S = zero-set 3 Q = G.V 4 while Q != zero-set 5 u= extract-min(Q) 6 S= S U {u} 7 for each vertex v in G.Adj[u] 8 Relax(u,v,w)
s ---> x ->y가 shortest path이므로, $x$가 $S$에 add 되면서 x->y에 relaxation할 때, y.d에 $δ(s, y)$가 저장. 따라서 $u$가 $S$에 add가 될 때에도 y.d = δ(s, y).
- y.d = \delta(s,y)
  - u.d \leq \delta(s,y) \leq u.d \rightarrow \delta(s,u) = u.d
- y.d = \delta(s,y) \leq \delta (s,u) \leq u.d
- u.d \leq y.d

# An O(n^2) Implementation : Adjacency Matrix 사용

S: the set of vertices, including v_0, whose shortest paths have been found
distance[w]: the length of the shortest path starting from v_0, going through vertices only in S, and ending in w (w \notin S)
Observations
- When the shortest paths are generated in nondecreasing order of length,
- If the next shortest path is to vertex u, then the path from v_0 to u goes through only those vertices that are in S.
- Vertex u is chosen so that it has the minimum distance distance[u] among all the vertices \notin S.
- Adding u to S may change the distance of shortest paths starting at v_0 going through vertices only in the new S, and ending at a vertex w that is not currently in the new S.
- distance[w] = \min \{distance[w], distance[u] + length(<u, w>) \}
V = \{ v_0, v_1, ..., v_{n-1}\} with |V| = n
distance[i] : the length of the SP from vertex v to i
found[i]
- FALSE if the SP from vertex i has not been found,
- TRUE otherwise
cost[i][j] : cost adjacency matrix

code in [Horowitz]

int choose(int distance[], int n, int found[])
{
    int i, min = INT_MAX,
          minpos = -1;
    for (i = 0; i < n; i++) // O(n)
        if (distance[i] < min && !found[i])
        {
            min = distance[i];
            minpos = i;
        }
    return minpos;
}
void shortestpath(int v,
                  int cost[][MAX_VERTICES],
                  int distance[], int n, int found[])
{
    int i, u, w, tmp;
    for (i = 0; i < n; i++)
    {
        found[i] = FALSE;
        distance[i] = cost[v][i];
    }
    found[v] = TRUE;
    distance[v] = 0;
    for (i = 0; i < n - 2; i++)
    { // O(n)
        // find the next u to be added to S
        u = choose(distance, n, found);
        found[u] = TRUE; // add u to S for (w = 0; w < n; w++)
        if (!found[w])   // for w not in S
        if ((tmp = distance[u] +
    }
}
cost[u][w]) < distance[w]) distance[w] = tmp;

# An O(e \log n) Implementation: Adjacency List 사용

매 순간 $wt[w]$에는 항상 S_k 의 꼭지점들만 사용할 경우에 대한 $v_s$에서 $w$까지의 shortest path의 길이가 저장되어 있음.
wt[]는 앞의 프로그램에서의 distance[]에 해당

n = |V|, e = |E|

typedef struct node \*link;
struct node
{
    int v;
    double wt;
    link next;
};
struct graph
{
    int V;
    int E;
    link *adj;
};
typedef struct graph *Graph;

#define GRAPHpfs GRAPHspt
#define P(wt[v] + t->wt) 
void GRAPHpfs(Graph G, int s, int st[],​ double wt[]){

  int v, w;
  link t;
  PQinit();
  priority = wt;
  for (v = 0; v < G->V; v++){ //O(n)
    st[v] = -1;
    wt[v] = maxWT;
    PQinsert(v);
  }
  wt[s] = 0.0;
  PQdec(s); // log n
  while (!PQempty())// 언제 끝날까?
    if (wt[v = PQdelmin()] ! = maxWT) //어떤 경우인가?
      for (t = G->adj[v]; t != NULL; t = t->next) //O(e log n)
        if (P < wt[w = t->v]){
          wt[w] = P;          
          PQdec(w); //log n
        //다 끝난 후 각 꼭지점에 대한 sp를 어떻게 출력할까?
          st[w] = v;  
        }
    }
}

MO ̈HRING et at., Partitioning Graphs to Speedup Dijkstra’s Algorithm, ACM Journal of Experimental Algorithmics, 2006.
- Standard Dijkstra’s Algorithm
- Acceleration Algorithm

alg