#
6.2. Graph Search
In
#
Some Problems Related to Graph Search
- Cycle detection
- Does a given graph have any cycle?
- Simple path
- Given two vertices, is there a path in the graph that connects them?
- Simple connectivity
- Is a graph connected?
- Two-way Euler tour
- Find a path that uses all the edges in a graph exactly twice – once in each direction.
- Spanning tree
- Given a connected graph with n vertices, find a set of n-1 edges that connects the vertices.
- Vertex search
- How many vertices are in the same connected component as a given vertex?
- Two-colorability, bipartiteness, odd cycle
- Is there a way to assign one of two colors to each vertex of a graph such that no edge connects two vertices of the same color?
- Is a given graph bipartite?
- Does a given graph have a cycle of odd length?
- st-connectivity
- What is the minimum number of edges whose removal will separate two given vertices s and t in a graph?
- General connectivity
- Is a graph k-connected?
- Is a given graph k-edge connected?
- What is the edge connectivity and the vertex connectivity of a given graph?
- Shortest path
- Find a shortest path in the graph from v to w.
- Single-source shortest paths
- Find shortest paths connecting a given vertex v with each other vertex in the graph.
#
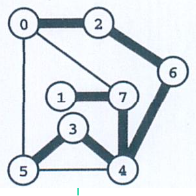
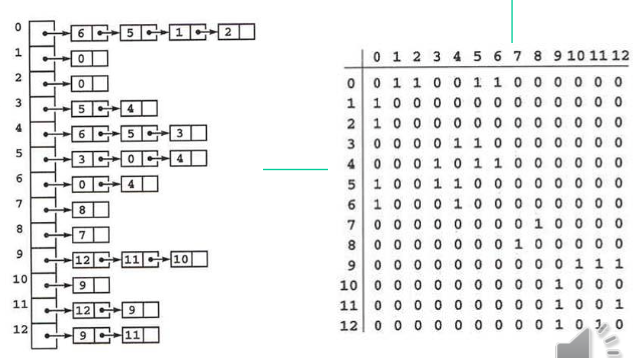
1) Graph Search 1: Depth-First Search (DFS)
- 자료구조 과목에서 배웠음

#
Depth-First Search: Review
A graph structure definition

typedef struct _edgenode { int y; /* adjancency info */ int weight; /* edge weight, if any */ struct _edgenode *next; /* next edge in list */ } edgenode; typedef struct _graph{ // The vertices are numbered starting from 1 not 0. edgenode *edges[MAXV + 1]; /* adjacency info */ int degree[MAXV + 1]; /* outdegree of each vertex */ int nvertices; /* number of vertices in the graph */ int nedges; /* number of edges in the graph */ int directed; /* is the graph directed? */ } graph;A Recursive implementation in C
- parent = predecessor
- entry time = discovery time
- exit time = finish time
void dfs(graph *g, int v) { edgenode *p; /* temporary pointer */ int y; /* successor vertex */ entry_time[v] = ++time; PROCESS_VERTEX_EARLY(v); discovered[v] = TRUE; p = g->edges[v]; while (p != NULL) { y = p->y; if (discovered[y] == FALSE) { parent[y] = v; PROCESS_EDGE(v, y, g); dfs(g, y); } else PROCESS_EDGE(v, y, g); p = p->next; } exit_time[v] = ++time; PROCESS_VERTEX_LATE(v); processed[v] = TRUE; }

#
An Abstract Implementation Using a Stack
- 편의상 connected graph로 가정 (아닐 경우에는?)
- 어떤 연산이 전체 탐색을 dominate하는가?
- 각 꼭지점은 unvisited 상태에서 스택에 몇 번 push되는가?
- 전체적으로 각 edge는 몇 번 access되는가?
DFS(G, s)
{ // s is the vertex where the DFS starts. Initialize a stack S to be empty;
visited[v] = F for all vertices in G;
Push(S, s);
while (S is not empty)
do{
v = Pop(S);
if (visited[v] = F){
visited[v] = T;
for (each vertex u that is adjacent to v)
if (visited[u] = F)
Push(S, u);
}
}
}- Time complexity
- Adjacency list: O(|V|+|E|)
- Adjacency matrix: O(|V|2)
- 기존에 배운 recursion 기반 구현과 비교할 것
#
3) Graph Search 2: Breadth-First Search (BFS)
자료구조 과목에서 배웠음

#
An Abstract Implementation Using a Queue
- 편의상 connected graph로 가정 (아닐 경우에는?)
- 어떤 연산이 전체 탐색을 dominate하는가?
- 각 꼭지점은 unvisited 상태에서 스택에 몇 번 push되는가?
- 전체적으로 각 edge는 몇 번 access되는가?
void BFS(G, s)
{ // s is the vertex where the DFS starts. Initialize a queue Q to be empty;
visited[v] = F for all vertices in G;
visited[s] = T;
Insert(Q, s);
while (Q is not empty){
v = delete (Q);
for (each vertex u that is adjacent to v) {
if (visited[u] = F){
visited[u] = T;
Insert(Q, u);
}
}
}- Time complexity
- Adjacency list: O(|V|+|E|)
- Adjacency matrix: O(|V|^2)