# 5.7. Scheduling with Deadlines

In

# Problem

Let J = \{1, 2, ..., n\} be a set of jobs to be served.
Each job takes one unit of time to finish.
Each job has a deadline and a profit.
- If the job starts before or at its deadline, the profit is obtained.
Schedule the jobs so as to maximize the total profit (not all jobs have to be scheduled).

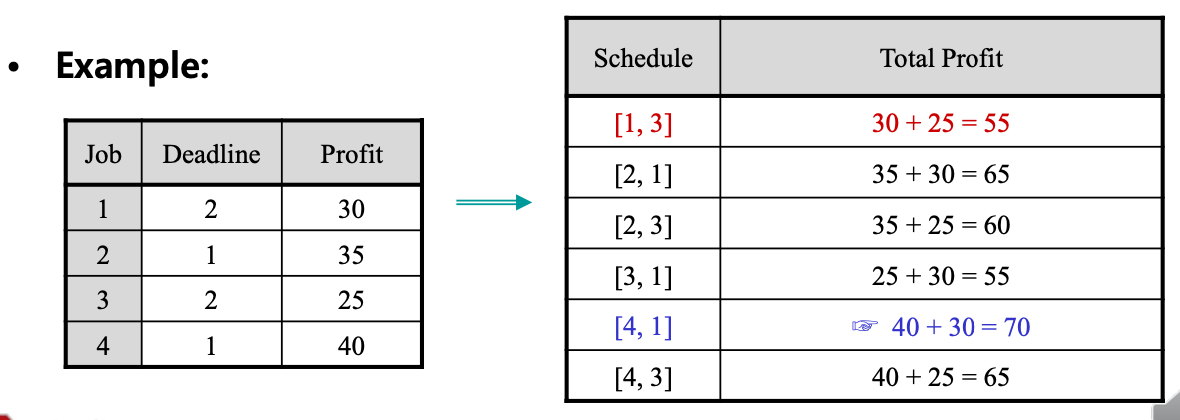
# Example:

# A greedy approach

Sort the jobs in non-increasing order by profit.
Scan each job in the sorted list, adding it to the schedule if possible.

# Example

S = EMPTY
Is S = {1} OK?
- Yes: S \leftarrow {1} ([1])
Is S = {1, 2} OK?
- Yes: S \leftarrow {1, 2} ([2, 1])
Is S = {1, 2, 3} OK?
- No.
Is S = {1, 2, 4} OK?
- Yes: S \leftarrow {1, 2, 4} ([2, 1, 4] or [2, 4, 1])
Is S = {1, 2, 4, 5} OK?
- No.
Is S = {1, 2, 4, 6} OK?
- No.
Is S = {1, 2, 4, 7} OK?
- No.

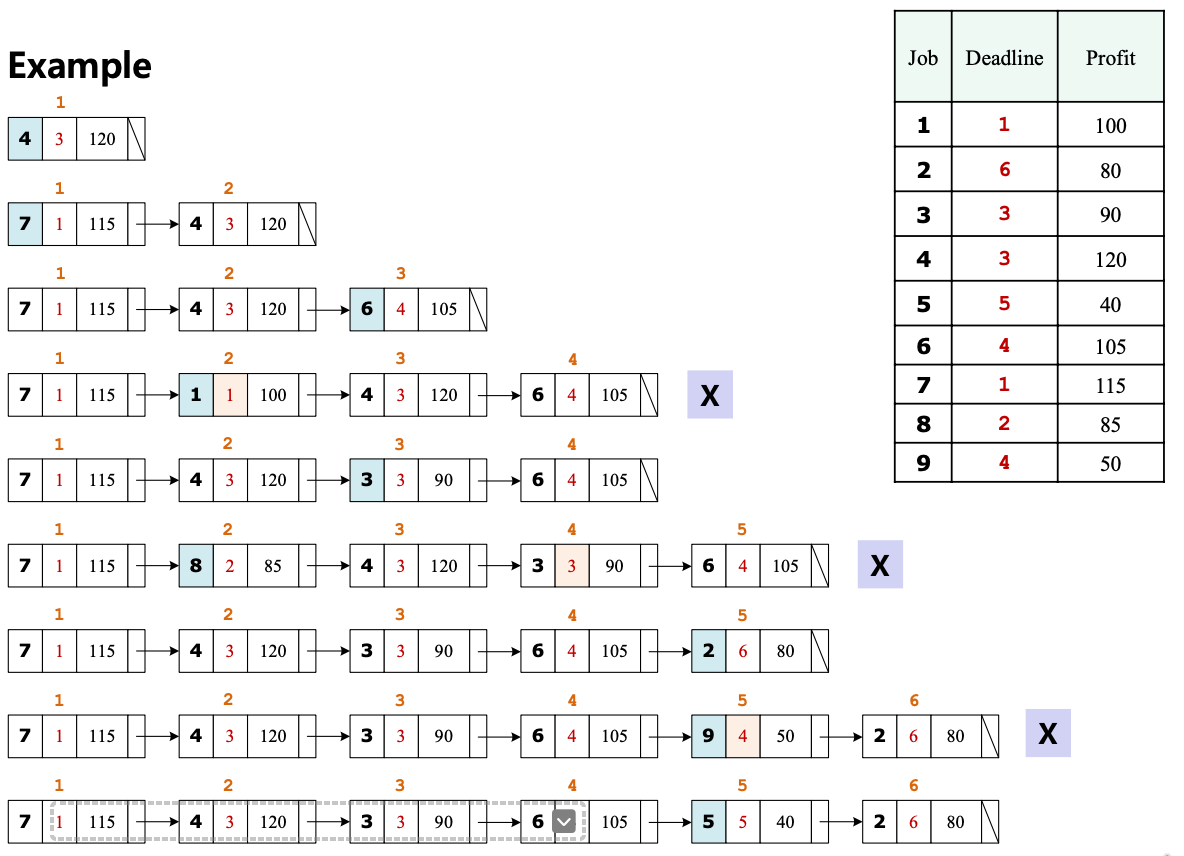
# Example

# Implementation Issues

A key operation in the greedy approach
- Determine if a set of jobs S is feasible.
- Fact
  - S is feasible if and only if the sequence obtained by ordering the jobs in S according to nondecreasing deadlines is feasible.
- Example
  - Is S = \{1, 2, 4\} OK?→$[2(1), 1(3), 4(3)]$→Yes!
  - Is S = \{1, 2, 4, 7\} OK?→$[2(1), 7(2), 1(3), 4(3)]$→No
An $O(n^2)$implementation
- Sort the jobs in non-increasing order by profit.
- For each job in the sorted order,
  - See if the current job can be scheduled together with the previously selected jobs, using a linked list data structure.
    - If yes, add it to the list of feasible sequence.
    - Otherwise, reject it.
- Time complexity
  - O(n \log n) + \Sigma_{i=2}^{n}{\{(i-1)+i\}} = O(n^2)
  - When there are i-1 jobs in the sequence,
    - at most i-1 comparisons are needed to add a new job in the sequence, and
    - at most i comparisons are needed to check if the new sequence is feasible.
Is the time complexity always O(n^2)?
- What if n >> d_{max}?
  - O(n \log n+n d_{max})
- What if n >> d_{max} and n >> k_{scanned}?
  - O(n + k_{scanned} \log n + k_{scanned} d_{max}) = O(n)
  - Is this complexity achievable when a max heap data structure is employed

# Correctness of the Greedy Method

Left as an exercise.

alg