#
1.3. Order of Algorithms
#
O (Big O Notation)
for given two functions f(n) and g(n) ,
g(n) = O(f(n)) \iff \exists c \in \mathbb{R}, N \in \mathbb{N}\quad
- s.t. \quad g(n)\leq c\cdot f(n) \forall n \geq N
then we say that : g(n) is big O of f(n)
x = x + 1;
for (i = 1; i <= n; i++)
y = y + 2;
for (i = n; i >=1; i--)
for (j = n; j >= 1; j--)
z = z + 1;정답 : g(n) = c_0 + c_1 n + c_2 n^2
예 : g(n) = 5 + 6 + 7n^2 \leq 8n^2 \quad \forall n \geq 8
- g(n) = O(n^2)
#
Notes for big O
[Note 1] The big O puts an asymptotic upper bound on a function.
Asymptotic analysis (from Wikipedia)
If f(n) = n^2 + 3n, then as n becomes very large, the term 3n becomes insignificant compared to n^2. The function f(n) is said to be "asymptotically equivalent to n^2, as n → ∞". This is often written symbolically as f(n) ~ n^2, which is read as "f(n) is asymptotic to n^2".
계산 비용이 0.01n^2 과 100n 알고리즘 중 어떤 것이 더 효율적인가?
(Tight) upper bound
- 37log n + 0.1n = O(n)
- n2 + 10n = O(n^2)
- $4(log n)^2 + nlog n + 100n = O(nlog n) $
- n^2 + 10n = O(n^200) ???
Growth Rates of Some Common Complexity Functions
[Note 2] Given a cost function g(n), how do you find the proper complexity function f(n) such that g(n) = O(f(n))?
- Suppress lower-order terms and constant factors!
- Example:
10^3 + 10^3n + 10^-3 n^2 = O(n^2)
- then lim_{n \to \infty} \frac{n^2}{n} = \infty
5nlog_3 n + 3(log_2 n)^2 + n + 6n^2 = O(n^2)
- then lim_{n \to \infty} \frac{n}{log_en} = lim _{n \to \infty} = \infty
3(log_2 n)^2+ 0.1n = O(?)
2^{n+5} = O(2^n) ??
2^{5n} = O(2^n) ??
#
Comparing Orders of Growth
- How do you compare orders of growth of two functions?
One possible way is to compute the limit of the ratio of two functions in question.
x = lim_{n \to \infty } \frac{f_1(n)}{f_2(n)}
- if x=0, f_1 has a smaller order of growth than f_2
- if x=c, f_1 has a same order of growth than f_2
- if x=\infty, f_1 has a larer order of growth than f_2
Ex.1: log_2 n vs \sqrt{n}
- $lim_{n \to \infty} \frac{\sqrt(n)} = lim_{n \to \infty} \frac{(log_2 n)'}{(\sqrt(n))'} = lim_{n \to \infty} \frac{(log_2 e)\frac{1}}{\sqrt\frac{1}{2\sqrt(n)}} = $
Ex.2: n! vs 2^n
- lim_{n \to \infty} \frac{ n!}{2^n} = lim_{n \to \infty} \frac{\sqrt{2 \pi n} (\frac {n}{e})^n}{2^n}=lim_{n \to \infty }\sqrt{2 \pi n} \frac{({n})^n}{2^n e^n}
- stirling's formula : n! \approx \sqrt{2 \pi n} (\frac {n}{e})^n
#
\Omega (Big Omega Notation)
for two given functions f(n) , g(n)
g(n) = \Omega(f(n)) \iff \exists c \in \mathbb{R} and N \in \mathbb{Z^+ \cup {0}}
s.t. g(n) \geq cf(n) \forall n \geq N
We say that g(n) is \omega of f(n) .
The \Omega puts an asymptotic lower bound on a function.
Ex:
- 37logn+0.1n=\Omega(n)
- n^2 + 10n = \Omega(n^2)
- 4(logn)^2 +nlogn+100n=\Omega(nlogn)
- n^{200} +10n=\Omega(n^2)...

#
\Theta (Big Theta Notation)
for two given functions f(n) , g(n)
g(n) = \Theta(f(n)) $\iff $ $g(n) = O(f(n)) $ and g(n) = \Omega (f(n))
that is,
$g(n) = \Theta (f(n)) $ \iff \exists c,d \in \mathbb{R} and N \in \mathbb{Z^+ \cup {0}} s.t. g(n) \geq cf(n) $ \forall n \geq N$
We say that g(n) is order of f(n).
The \Theta puts an asymptotic bound on a function.
Ex:
- 37logn+0.1n=\Theta(n)
- n^2 + 10n = \Theta(n^2)
- 4(logn)^2 +nlogn+100n=\Theta(nlogn)
\Theta(1)<\Theta(log n)<\Theta(n)<\Theta(n log n)<\Theta(n^2)<\Theta(n^3)<\Theta(n^j)<\Theta(n^k)<\Theta(a^n)<\Theta(b^n)<\Theta(n!)
- for $ k>j>3$ and b>a>1
- O(1) or O(c) : constant
- $g(n) = 0.000001 \cdot n $
- g(n) = 1000000
Ref. Neapolitan Ex. (pp.42) 19, 24, 26, 28]
#
Big O, Omega, and Order

Ref. [ Neapolitan Chapter 1.]
Execution Times for Algorithms with the Given Time Complexities
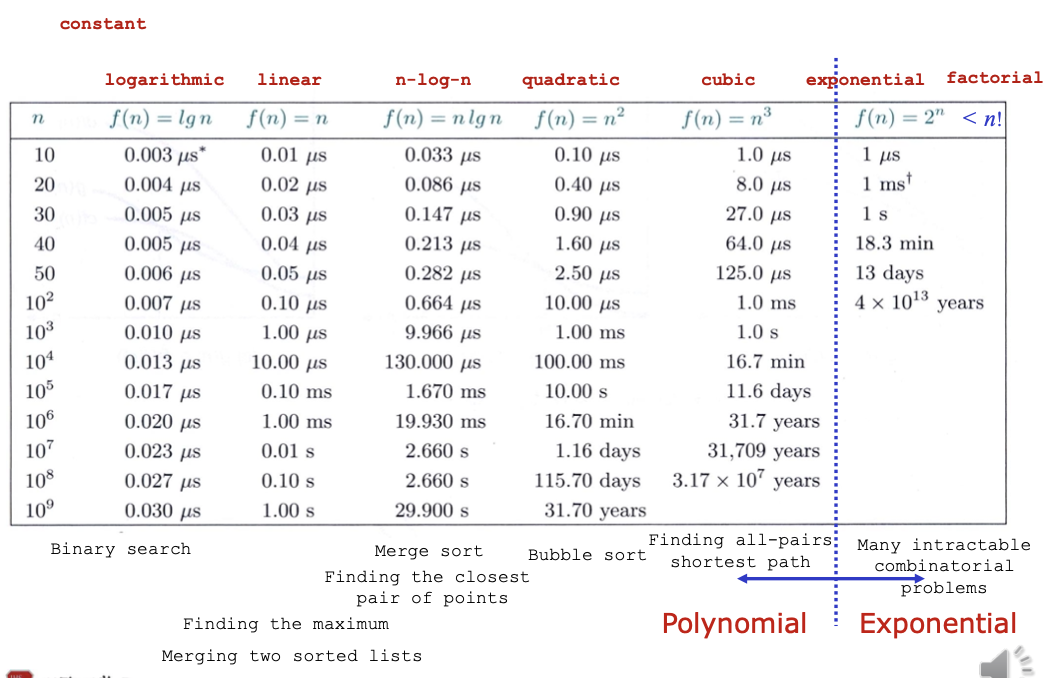
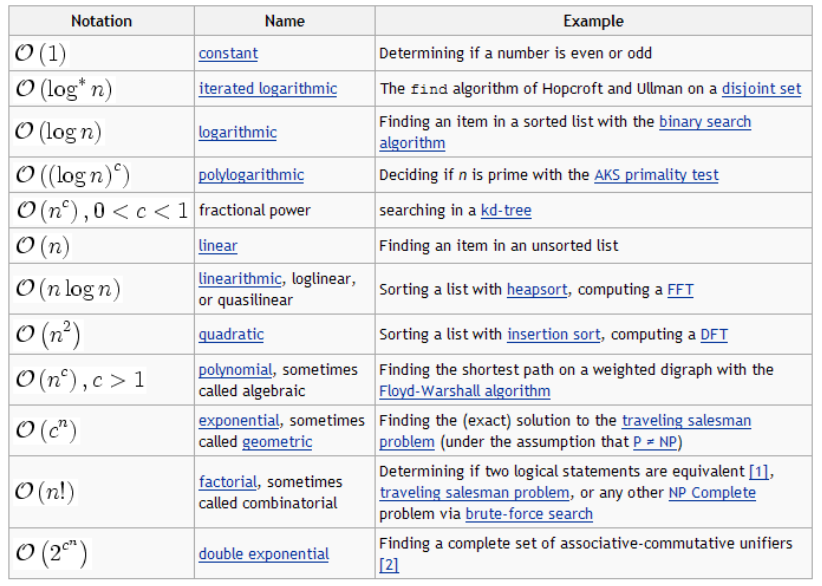
#
Worst-Case versus Average-Case Time Complexity
Expected value (from Wikipedia)
let X be a random variable with a finite number of finite outcomes x_1, x_2, ..., x_k occuring with probabilities p_1, p_2, ... p_k respectively.
the Expectation of X is defined as : E(X) = \sum_{i=1}^{k }{x_i p_i} = x_1p_1+ x_2 p_2 + ... + x_k p_k
since the sum of all probabilities p_i is 1 (\sum_{i=1}^{k} {p_i}=1) , the expected value is the weighted sum of the x_i values, with the p_i values being the weights
Worst-case complexity
- T_W (n) = max \{ c(I)| I \in S_n \}
Average-case complexity
- $T_A (n) = \sum_{I \in S_n} p(I) c(I) $
Problem
- Find the index of a given value a in a givven array (a_0, a_1, ...,a _{n-1}). if a doesn't exist in the array return -1
Cost for a linear search algorithm
let P_i be the probability such that a= a_i
then the average cost is :
g(n) = 1 \cdot P_0 + 2 \cdot P_1 + 3 \cdot P_2 + ...+ n \cdot P_{n-1} + n (1 - \sum_{k=0}^{n-1} P_k)
= \sum_{k=0}^{n-1} (k+1)P_k + n (1 - \sum_{k=0}^{n-1} P_k)
Ex.1. n = 10^9, P_0 + P_1 + ...+ P_{10^3} = 1 so g(n) = O(1)
Ex.2. n = 10^9, P_0 + P_1 + ...+ P_{\frac n {100} }= 1 so g(n) = O(n)
참고: Quick sort 알고리즘 →
- Worst-case O(n^2),
- Average-Case O(n log n)
#
Reviews
#
Summation
Sums of powers
- \sum_{i=1}^{n} i = \frac {n(n+1)} {2}
- \sum_{i=1}^{n} i^2 = \frac {n(n+1)(2n+1)} {6}
- \sum_{i=1}^{n} i^3 = (\frac {n(n+1)} {2})^2
- \sum_{i=1}^{n} i^4 = \frac {n(n+1)(2n+1)(3n^2+3n-1)} {30}
- \sum_{i=1}^{n} i^s = \frac {(n+1)^{s+1}} {s+1} + \sum_{k=1}^{s} \frac {B_k} {s-k+1} {s \choose k} (n+1)^{s-k+1}
- B_k is the k^{th} Bernoulli Number.
- \sum_{i=1}^{n} i^{-s} = \prod_{p prime} \frac {1} {1 - p^{-s}} = \zeta(s)
- \zeta_k is the Riemann zeta function
Growth rates
\sum_{i=1}^{n} i^c \in \Theta(n^{c+1}) for real c greater than -1
\sum_{i=1}^{n} \frac 1 i \in \Theta(log n)
\sum_{i=1}^{n} c^i \in \Theta( n \cdot log(n)^{c+1}) for real c greater than 1
\sum_{i=1}^{n} log(i)^c \in \Theta(n \cdot log(n)^{c}) for nonnegative real c
\sum_{i=1}^{n} log(i)^c \cdot i^d \in \Theta(n^{d+1} \cdot log(n)^{c}) for nonnegative real c, d
\sum_{i=1}^{n} log(i)^c \cdot i^d \cdot b^i \in \Theta(n^{d} \cdot log(n)^{c} \cdot b^n) for nonnegative real b>1, c, d
Read Summation, Mathematical Series
#
Run Time Analysis
What is the worst-case time complexity of each loop?
(1) Matrix Addition
for (i = 0; i < N; i++) for (j = 0; j < N; j++) a[i][j] = b[i][j] + c[i][j];(2)
x = 0; for (i = 1; i <= N; i++) for (j = 1; j <= i; j++) x += i + j;(3)
for (i = 1; i <= N; i++)
if (i % 2 == 0) a[i] = 1;
else a[i] = -1;
for (i = 1; i <= N; i++)
for (j = 1; j <= N; j++)
a[i][j] = i + j;- (4)
for (i = 1; i <= N; i++) {
if (i % 2) {
for (j = 1; j <= N; j++)
a[i][j] = i + j;
}else {
for (j = 1; j <= N; j++) {
a[i][j] = 0;
for (k = 1; k <= N; k++)
a[i][j] += k;
}
}
}(5)
x = 0; for (i = 1; i <= N; i++) for (j = 1; j <= i; j++) //What if this is i*i? for (k = 1; k <= j; k++) x += i + j + k;(6) \rightarrow O(N^4)
x = 0; for (i = 1; i<=N;i++) for (j = 1; j <= i*i; j++) if (j % i == 0) for (k = 1; k <= j; k++) x++;
What is the worst-case time complexity of each loop?
(1)
// n = 2^k for some positive // integer k for (i = 1; i < N; i++) { j = n; while (j >= 1) { // some O(1) computation j = j/2; } }(2)
// n = 2^k for some positive // integer k i = n; while (i >= 1){ j = i; while (j <= n){ // some O(1) computation j = 2*j; }i = i/2; }(3) Could this be faster?
// float x[n][n+1]; for (i = 0; i <= n-2; i++) for (j = i+1; j <= n-1; j++) for (k = i; k <= n; k++) x[j][k] = x[j][k] – x[i][k]*x[j][i]/x[i][i];(4) Magic square : Could this be faster?
// n: odd integer for (i = 0; i < n; i++) for (j = 0; j < n; j++) s[i][j] = 0; s[0][(n-1)/2] = 1; j = (n-1)/2; for (key = 2; key <= n*n; key++) { k = (i) ? (i-1) : (n-1); l = (j) ? (j-1) : (n-1); if (s[k][l]) i = (i+1)%n; else { i = k; j = l; } s[i][j] = key; }(5) O(\log n)
// compute x^n (n >= 0) m = n; power = 1; z = x; while (m > 0) { while (!(m%2)) { m /= 2; z *= z; }m--; power *=z; }time complexity. : c_0 + c_1 n + c_2 n^2 = O(n^2)
x = x + 1; for (i = 1; i <= n; i++) y = y + 2; for (i = n; i >=1; i--) for (j = n; j >= 1; j--) z = z + 1;time complexity. : c( ⌊{log_2 n}⌋+1) \cdot n^2 = O(n^2)
c = 0; // n > 0 for (i = 1; i <= n; i++) for (j = 1; j <= n; j++) for (k = 1; k <= n; k = k*2) c += 2;time complexity. : ??= O( \sqrt n)
i = 1; j = 1; m = 0; // n > 0 while (j <= n) { i++; j = j + i; m = m + 2; }
